バドミントンデータ解析ブログ

バドミントンについて、しょーもないことも含めてデータ解析で遊びます。主にTwitter(@badiary09)に生息しています。

スコアリングシステムの変更は弱小国に有利

先に結論をタイトルに書いてみました．

BWF（世界バドミントン連盟）がスコアリングシステムをラリーポイント制21点3ゲームからラリーポイント制11点5ゲームに変更することを検討していて，その理由として

  • 競技時間の短縮
  • より試合を面白くする

ことを挙げています．このうち，競技時間についてはラリーポイント制の導入時から年々長くなっていることを以前に確認しました（はてなブログ，Rpubs）．

ところで，ルールの変更と言えば政治的な意図が含まれていることを疑いたくなりますね．仮に11点5ゲームに変更された場合，どの国に有利に働くのでしょうか，気になります．もうタイトルに結論書いたけど．

Magnification Effect

今回の調査にあたって重要なのは"Magnification Effect"と呼ばれるものです．ここでは適当に増幅作用と訳しておきますが，増幅作用とはテニスにおいて提唱された概念です（参考論文）．

プレーヤーAとBがバドミントンで対戦しているとします．そして，どのラリーにおいてもプレーヤーAが勝つ確率がpであるとします．この時，Aの方が強い（p>0.5）ならばAがゲームを取る確率や試合に勝つ確率はpよりも更に大きくなります．これを増幅作用と呼びます．直感的には，「マッチポイントが多くなればなるほど，最終的に強いプレーヤーが勝つ確率が高くなる」というものです．

例えば，僕がLee Chong Wei（世界1位）と戦ったとします．1点マッチと21点マッチではどちらが僕の勝つ見込みが高いでしょうか．答えは1点マッチです．1点ならまぐれで勝てるかもしれませんが，21点もまぐれが連続することはほとんどありません．

スコアリングシステムによって増幅作用の大きさは変わるので，スコアリングシステムが変われば強者と弱者のどちらかが喜ぶわけです．もちろん，強者より弱者の方が勝率が高くなるなんてことはないですが．

勝率の算出

それでは実際に勝率を求めてみます．プレーヤーAとBが対戦していて，AとBはそれぞれサーブ時に p_A, p_Bの確率でラリーに勝つものとします．二つの確率を導入するのは，バドミントンがレシーバーに有利と思われるからです（関連記事）．

ゲームは0-0，Aのサーブから始まるものとします．この時，スコアm-nを通過する確率を，その時Aがサーブする場合 S_A (m,n)とBがサーブする場合 S_B (m,n)に分けて考えます．これらはmとnに関する漸化式で求めることが出来ます．

\displaystyle{ S_A (m,n) = p_A S_A (m-1,n) + (1-p_B) S_B(m-1,n) } \displaystyle{ S_B (m,n) = (1-p_A) S_A (m,n-1) + p_B S_B(m,n-1) }

後は初期条件 S_A(0,0)=1, S_B(0,0)=0を使ってがしがし計算していき，最終的にAが勝っている状態の確率を全て足し合わせることでAがゲームを取得する確率（これを P_A ^{(g)}とします）を求めることが出来ます．

実際にはMathematicaで求めました．21点の場合の解の一部を見てもらえれば，手計算では不可能なレベルであることが分かると思います．最も高次の項は p_A ^{30} p_B ^{29}であり，適当に計算したのでは数値誤差で計算機ですら結果が正しく求まりません． f:id:tenjin7:20150306220125p:plain

P_A ^{(g)}が分かってしまえば，Aが試合に勝つ確率を求めるのは簡単です．（面倒なので省略）

Aがゲームを取る確率のプロット

勝率を求めたので早速プロットといきたいんですが，その前に変数を新たに定義します．

\displaystyle{ p_{+} \equiv p_A + p_B }

\displaystyle{ p_{-} \equiv p_A - p_B }

前者は両者に共有したサーバー側の有利度合いを，後者は実力差を表します．変数を p_A, p_Bよりもこの二つにした方がプロットが見やすくなります．

さて，それではAがゲームを取る確率を見てみます．p+を固定してp-を動かしたものが以下の図です．

f:id:tenjin7:20150306221846p:plain

f:id:tenjin7:20150306221853p:plain

f:id:tenjin7:20150306221858p:plain

グラフは全てS字になっており，確かに増幅作用が存在することが分かります．また，21点3ゲームの方が11点5ゲームよりも増幅作用が強いです．当たり前ですね．

一方，p+を固定してp-を動かしたものが以下の図です．

f:id:tenjin7:20150306222333p:plain

f:id:tenjin7:20150306222340p:plain

どれもp+に対して単調減少しています．つまり，サーバー側が有利な競技であればあるほど弱者の勝つチャンスが増えるということです．点を取った方がサーバーになるということから，サーバーに有利なほど連続得点のチャンスが増え，勢いで勝ってしまう可能性が増えるということだと解釈できます．

Aが試合に勝つ確率のプロット

次に，本題であるAが試合に勝つ確率を見てみます．p+を固定してp-を動かしたものが以下の図です． f:id:tenjin7:20150306222830p:plain

f:id:tenjin7:20150306222836p:plain

f:id:tenjin7:20150306222842p:plain

Aがゲームを取る確率に比べると二本の曲線は接近していますが，それでもやはり21点3ゲームの方が増幅作用が強く，強者に有利であることが分かります．

一方，p+を固定してp-を動かしたものが以下の図です．

f:id:tenjin7:20150306223014p:plain

f:id:tenjin7:20150306223021p:plain

両者の実力が拮抗している時ほど二本の曲線の差が強くなりました．つまり，実力の近い選手同士の対戦ほどスコアリングシステムの改正の影響を受けやすいということです．

結論

11点5ゲームは21点3ゲームに比べて弱小国にプラスに働きます．政治的な意図を深読みするのなら，アジアの勢力が強い状況にヨーロッパ勢力が危機感を抱き，試合時間の短縮という大義名分もできて丁度良いのでスコアリングシステムの変更に向けて動いている，といった感じでしょうか．

今後の課題

本当はサーブ制15点3ゲームも比較対象に入れたかったのですが，勝率の計算に複雑な無限和が入ってきたので計算を諦めました．誰か助けて下さい．

バドミントンはサーバーとレシーバーどちらが有利か

タイトルの通りです．テニスはサーバー有利，バレーボールはレシーバー有利ということになっていますが，バドミントンはどちらなのかを調べてみました．

調査方法

単純に全ラリーのうちサーバーとレシーバーの勝率を比較しても正しい結果は得られません．なぜなら，ラリーの勝者が次のサーバーになるというルールであり，その結果強い選手ほどサーバーになりやすく，サーバーの勝率が高く見積もられてしまうからです．今知りたいのは，選手の実力差によらず，一般的にバドミントンという競技はサーバーとレシーバーにどのようなハンディが存在するのかということです．

この問題は，実力によってサンプル数が偏ってしまうことに起因しています．そこで，次のように調べることにしました．

  1. プレーヤーAとBが戦った一試合に注目する．
  2. Aがサーブの時にAが点を取った割合を p_s ^{(A)} ，Bがサーブの時にBが点を取った割合を p_s ^{(B)} としてそれぞれ計算する．
  3. 過去全ての試合（ N試合とする）について p_s ^{(A)} と p_s ^{(B)} の平均 p_s ^{(mean)} を求める．{ \displaystyle p_s ^{(mean)} = \frac{1}{2N} \sum_{全試合} \left( p_s ^{(A)} + p_s ^{(B)} \right) }

3.においては，プレーヤーの区別はせず，とにかく全試合の平均を取ります．つまり，AとBにはその都度色々な人が対応するということです．このようにして求めた p_s ^{(mean)} を一般的なサーバーの勝率と解釈することにします．

相当荒っぽい求め方なのは重々承知していますが，この他に良い方法を思いつきませんでした．アイディア募集中！

データは2007年から2014年までのSuper Series，Grand Prix Gold，Grand Prixのランクの試合，全34652試合としました．今回は種目を区別して導出しました．

結果

まず，サーブ時の勝率 p_s （ p_s ^{(A)} 及び p_s ^{(B)} ）のヒストグラムを種目ごとにプロットしてみました． f:id:tenjin7:20150305225557p:plain f:id:tenjin7:20150305225605p:plain f:id:tenjin7:20150305225612p:plain f:id:tenjin7:20150305225623p:plain f:id:tenjin7:20150305225657p:plain

…特に何も考察できない気がします．

次に，本題の p_s ^{(mean)} を求めます．これは全体の平均で求めるので，ついでに標準偏差も求めてみました．

サーバーの勝率 p_s ^{(mean)} MS WS MD WD XD
平均 48.4% 47.7% 43.8% 46.2% 44.9%
標準偏差 12.8% 13.1% 12.1% 14.1% 12.2%

全ての種目でレシーバー有利，特にダブルスでそれが顕著であるという結果となりました．今回の求め方はかなり議論の余地がありますが，データ数が十分大きく，また推定バイアスはないんじゃないかと思っていることがあるので，レシーバーが有利であることは間違っていないのではと考えています．

結論

バドミントンは恐らくレシーバー有利です．しかし，テニスやバレーボールに比べるとそこまで大きな差はないようです．

先に11点を取ることは重要なのか？

全日本総合選手権を見ていると，解説の方が良く「先に11点を取ってインターバルを迎えることが重要なんです」と言っているのを聞きます．精神的に落ち着けるからというのがその根拠だと思うのですが，本当でしょうか．気になります．

という訳で，調べてみました．

調査方法

まず，「重要」の意味を定義しないといけません．基本的には「勝つために」重要だということだと思うので，そのゲーム（マッチではない）の勝率が上がるかどうかを調べるのが良いでしょう．という訳で，10対n（n<10）の時に一点を取ることは，他の局面に比べて勝率の上昇が大きいかどうかを調べます．

勝率の上昇は，次の流れで求めます．

  • 全てのm,nについて，m対nの時点での勝率を求める
  • (m+1)対nの勝率からm対(n+1)の勝率を引いた値を勝率の上昇分とする．（これをm対nにおける一点の重要性と定義する）

m対nの時点での勝率は，過去，m対nを通過した全てのゲームのうち，最終的にそのゲームを取った割合とします．データは，2007年から2014年までのSuper Series，Grand Prix Gold，Grand Prixのランクの試合，全34652試合としました．種目や性別は今回は特に区別しませんでした．

結果

まず，各スコアでの勝率を見てみます． f:id:tenjin7:20150304184502p:plain これは，横軸のプレーヤーAに焦点を当てた図です．赤いゾーンはAの勝率が高いということです．特異な点は見つからず，綺麗なデータになっている気がします．

次に，この勝率データから各スコアでの一点の重要性を求めたものが次の図です． f:id:tenjin7:20150304184510p:plain これを見ると，ゲームポイントに近いほど一点の重要性が高くなっています．これは当然ですね．また，点差が離れているほどその局面は重要でないという結果になっています．圧倒的な差があれば一点の出来事で結果はほとんど左右されないということで，こちらも直感に合います．

そして，11点の辺りに注目してみると…特に周囲と変わりないように見えます．つまり，この図からは11点が特別な点であることを読み取れません．

あっさりしていますが，これでお終い．

結論

今回の定義では，先に11点取ることは特に「重要」ではなさそうです．インターバルの効果は点差に関わらず公平に表れているということなのでしょうか．

20-20以降はシーソーゲームになりやすいか

陸上の長距離，特にマラソンなんかを見ていると，集団で走ることが多いですね．他者を風除けにしたいからという説明を良く見ますが，人間の心理も関係あるんじゃないかと思います．前の人に着いていくのは精神的に楽，みたいな．

バドミントンで似たような話を考えたいんですが，今回は20-20以降のスコアについて調べてみたいと思います．片方がマッチポイントを握った時に，もう片方がラリーに勝ってスコアを並べる確率を調べれば，シーソーゲームになりやすいかどうかを判定することが出来ます．

帰無仮説：状況によらずラリーの勝率は50%

今回は検定をするわけではないんですが，一応立てる帰無仮説は，どっちがマッチポイントを握っているかに関係なくラリーの勝率は50%であるというものです．つまり，心理状態なんて関係ねえってことですね．

20-20に達している時点で実力は互角としていいと思うので，何も影響がなければ勝率は50%になるでしょう．

使用データ

今回は2007年～2013年のGrand PrixからSuper Seriesまでのうち20-20を通過したゲーム，全5310ゲームです．

帰無仮説が正しければ，22-20の試合が全体の50%，23-21の試合が25%，…というように，勝者のスコアが1増える度に割合が半分になっていくはずです．表現を変えると，p=1/2の幾何分布に従うはず．

結果

最終スコア ゲーム数 割合
22-20 2646 49.83%
23-21 1242 23.39%
24-22 692 13.03%
25-23 345 6.49%
26-24 174 3.27%
27-25 92 1.73%
28-26 50 0.94%
29-27 35 0.66%
30-28 17 0.32%
30-29 17 0.32%

…順調に1/2の割合で減っていっている気がします．割合をデータと仮説上の値で比べてプロットしてみましょう．

f:id:tenjin7:20140721110547p:plain

うわー，すごく綺麗に当てはまっていますね．

分布が幾何分布に従っているかどうかの検定方法が分からないので，図を眺めておしまい．

結論

自分/相手がマッチポイントを握っていることは，次のラリーの勝率に特に影響を与えないようです．

個人個人を調べるととても影響される人，されない人がいるんでしょうが，全体としてはその影響はプラマイゼロになっているということなんでしょう．きっと．

ファイナルゲームでどちらが勝つか予測出来るか

三ヶ月前の話ですが，スポーツ安全国際センター（ICSS)という団体がスポーツに関係する賭博が広がっていることに関して警告を発しました（参考記事）．賭博の市場があまりにも広がっていて，世界全体のGDPの2%を占めているらしいです．凄いですね．そして，賭博が広がっているスポーツの中にバドミントンが含まれているんです．確かに"badminton betting"で検索すると結構ヒットしますね．

最近Lee/Yooがスーパーシリーズ3連勝を成し遂げましたが，これを全部当てていたら一体何倍ぐらいになっていたんでしょうか...気になります．いや，それよりオーストラリアオープンで大穴の橋本由衣がベスト4に入ったの当てる方がすごいか．あとは，日本のトマス杯優勝・ユーバー杯準優勝もオッズは高かったんじゃないだろうか...

とまあ色々と考えが止まらないんですが，賭博があるなら誰が勝つかの予測を当然したくなります．どうやらトーナメントの優勝者を予想するのがポピュラーらしいんですが，ちょっと問題が難しすぎるので，まずはとても簡単なところから始めたいと思います．

今回は，試合がファイナルに入った場合の勝者を予測出来るか考えてみます．

第1ゲーム勝者と第2ゲーム勝者，どちらが勝つか？

まずは第1ゲームと第2ゲームどちらを取っているかが勝率に影響するかどうかを調べてみます．今回は対象とするデータを2007年～2013年のGrand Prix以上の大会とします．

全27873試合の中でファイナルまでいった試合は8223試合（約30%），うち第1ゲームの勝者が勝ったのは3944試合，第2ゲームの勝者が勝ったのは4279試合でした．これを二項検定にかけてみます．

data:  c(3944, 4279) 
number of successes = 3944, number of trials = 8223, p-value
= 0.0002299
alternative hypothesis: true probability of success is not equal to 0.5 
95 percent confidence interval:
 0.4687804 0.4904947 
sample estimates:
probability of success 
             0.4796303

p値が0.0002ということで，勝率には有意に差があるようです．第1ゲームの勝者の勝率が48%程度でした．

良く試合前のじゃんけんで始めは風や照明の点から不利なコートを選んだ方がいいということを聞きます．ファイナルまでいけば有利なコートでプレーする時間が長くなるからですが，その影響が表れた結果なのかもしれません．

得失点差は勝率に影響するか？

第2ゲームまでの得失点差は勝率に影響するのでしょうか．調べてみます．まずは，得失点差とそこから勝った試合の数のヒストグラムを見てみましょう．

f:id:tenjin7:20140706000553p:plain

なんだか凄く綺麗な形になりました．一つ飛び抜けているのは得失点差が0の場合です．これをピークとして外側になるにつれ減少していっていますが，どうも分布が右に偏っている気がしますね．分布が左右対称なら得失点差は第3ゲームの勝率に影響しないということになるのですが，どうもそうではないようです．

次に，得失点差ごとの第3ゲームの勝率を見てみましょう．（得失点差が負の部分は正の部分をひっくり返しただけです．）

f:id:tenjin7:20140706002052p:plain

...おお！結構綺麗な線形関係になっていますね．単回帰分析をすると，1点につき1.9%程度勝率が変わるようです．5点離れると勝率が10%違うというのは驚きです．正直得失点差はあまり関係ないものだと思っていました．

ちなみに，先ほどのヒストグラムで見たように，得失点差ごとにサンプル数が違っています．±15点を超えると数試合程度しかデータがないので，勝率が暴れています．

本当は検定を行いたいところですが，サンプル数が違うためどうやってかけたらいいか分かりません．さっきの単回帰分析も，本当は重み付き最小二乗をしないといけないですね．統計に詳しい方，どなたかご教授して頂けないでしょうか...

結論

ファイナルゲームの勝率は得失点差に大きく影響しています．得失点差×1.9%に第1ゲームと第2ゲームどちらを取ったかの2%分を加味した結果を信じるといいんじゃないでしょうか（適当です）．

勢いとか流れといったメンタル的なことを考えるためには，各ゲームのスコアの推移まで考慮しないと駄目ですね．そちらも気になります．

試合時間が長くなってきている？

BWFが発表した21点3ゲーム制を見直すというニュースが話題になっています．

The 5x11 scoring system is aimed at creating more excitement and interest while reducing the time which matches take to be completed.

どうやら狙いは試合を面白くすることと試合時間の短縮にあるようです．

しかし，2006年にラリーポイント制が導入された時も同じような理由が挙げられていたように思います．そして，ラリーポイント制になって確かに試合時間が短くなったはずです．それなのにまだ足りないのでしょうか．

...などということを考えていたら，面白い情報を見つけました．曰く，ラリーポイント制の導入時に比べて最近は試合時間が伸びているらしいのです．ソースは2ch．

509 ：アスリート名無しさん：2014/06/21(土) 02:00:58.65 id:HcTbswWd
またルール変わるんか 
協議時間短縮って、今も別にアホみたいに長いわけじゃないのに 
なにがダメなんだ 

510 ：アスリート名無しさん：2014/06/21(土) 05:32:05.78 id:vie66NKG
いや間違いなく競技時間が伸びてきてる。サービスポイント時代と変わらないくらいに。 
なんでだろな。選手が間をとってダラダラ時間稼ぐせいもあるけれど。
（以下略）

これは検証するしかない！

調べてみました

2007年～2013年のSuper Series大会，全13886試合を対象に平均試合時間の推移を見てみます．

f:id:tenjin7:20140705185926p:plain

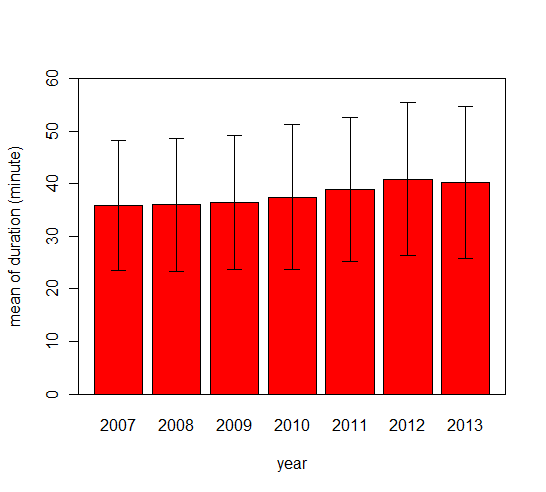
一応増えてますね．エラーバーは標準偏差を表していますが，こちらは平均の増加による効果以上にわずかに増加しています．

検定をしてみます．勝手に年度と試合時間の間に線形関係を仮定して，正の相関があるかをテストします．

 Pearson's product-moment correlation

data: data_SS$year and data_SS$duration 
t = 16.0943, df = 13884, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0 
95 percent confidence interval:
 0.1189674 0.1516240 
sample estimates:
 cor 
0.1353325

p値が2.2e-16以下ということで，間違いなく正の相関がありますね．相関係数は0.135程度の模様．

結論

試合時間は間違いなく伸びています．更に，今後はチャレンジシステムの導入があり更に伸びることが予想されます．なので，運営側の立場からするとスコアリングシステムを変えようという意見も分からなくはないですね．

ただ，数分程度の増加がテレビ放映に影響を持つのかは良く分かりません．テレビ放映に関しては試合時間云々というよりは21点が多いせいで序盤に緊張感がないのを変えたいというのがメインなのかもしれません（参考記事）．

それにしても，数年で数分程度の試合時間の伸びを察知していた2ちゃんねらはすごいですね．恐るべし．

おまけ

種目別に分けて考えると？

MS,WS,MD,WD,XDに分けて考えましょう．それぞれの2007年～2013年の試合の平均時間とその標準偏差です．

f:id:tenjin7:20140705185939p:plain

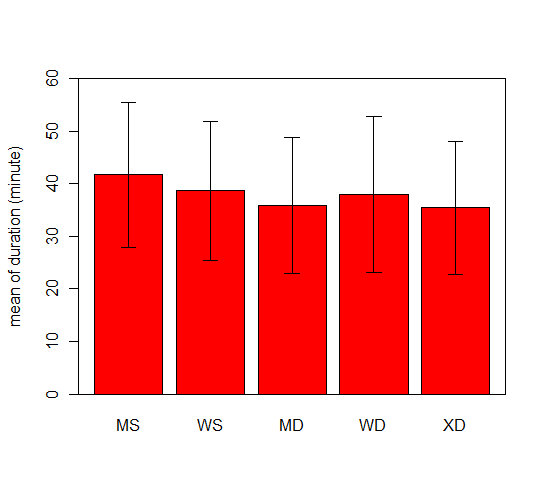
シングルスが長いですね．しかし，MSが一番長いというのは意外！てっきりWSが一番だと思っていました．ラリースピードは男子の方が速いはずなので，それにも増してラリーの回数が多いんですね．

ちなみに，種目別に無相関検定を行うと，MDだけ帰無仮説を棄却出来ません．つまりMDは試合時間が大して伸びてないんですね．最近のMDの試合はスマッシュの速度が上がっているせいですぐにどちらかがミスしてしまう印象がありますが，その表れでしょうか．

大会何日目かで分けて考えると？

Super Seriesのタイムテーブルを見ると，大会何日目かによって試合時間の見積もりを変えているようです．決勝に近づけば近づくほど実力が拮抗してくるはずなので，試合時間を長めに取るのは妥当でしょう．

こちらは何日目かと年に分けて平均時間だけ出してみました．見辛くてすみませんが，情弱で二次元棒グラフのやり方が分からないのでテキストデータで．

   year
day     2007     2008     2009     2010     2011     2012     2013
  1 33.46063 33.20385 35.29412 35.70813 37.39614 38.77778 38.14341
  2 38.28458 38.13681 37.18732 39.50515 41.13208 43.60218 43.02907
  3 38.49091 38.01081 40.23415 41.51429 43.75796 43.77778 45.86772
  4 42.63218 40.36458 43.20192 45.04706 44.92208 45.69149 44.78431
  5 40.83721 41.68750 45.09804 47.33333 45.31579 47.57778 48.19231
  6 41.50000 51.33333 45.03846 48.13636 44.16667 47.95833 53.26923
  7 38.50000 54.00000 49.00000 51.00000       NA       NA 51.00000

dayの数字がそのまま何日目かを表します．大会によって全日程数は異なるので，決勝と準決勝が同じdayに混ざっていたりします．NAがあるのは，2011年と2012年には7日間かけた大会が無かったということですね．

個別に気になるところはありますが，ひとまず全体的な傾向としてはやはり決勝に近づく程試合時間は長くなっていますね．また，何日目かによらずやはり過去に比べて試合時間が長くなっているということが言えると思います．

バドミントンの国際試合の結果を解析する準備が出来ました

やりたいこと

gg_hatanoさんの野球データ解析のブログを見て，いつか自分もバドミントンのデータを色々いじってみたいなと思っていて，その準備が整いました．

準備とは何かということなんですが，野球のようなメジャーなスポーツと違ってバドミントンはcsv形式でデータをダウンロード出来るなんてことがないので，自分でデータを集めて整理しないといけません．それが思いの外面倒で，時間を食ってしまいました．

データ収集元のサイトはtournamentsoftwareです．BWF管轄の大会の試合結果は全てこのサイトで公開されています．例えば，今年始めのKorea Openのページではこんな感じに結果が公開されています．

f:id:tenjin7:20140524195459p:plain

各試合ごとに，次のようなスコアの推移も公開されています．

f:id:tenjin7:20140524195720p:plain

これらのデータを解析し易い形で集めたい，という訳です．

プログラミング

ここからはプログラミングのお時間です．webサイトの情報を自動収集したいということで，Pythonでwebクローラを書くことにしました．Pythonで収集したデータは，そのままPythonからMySQLを呼び出し，そこにデータを保存するという形を取ります．その後，RからMySQLを呼び出して収集したデータを取り出し，解析をすることにしました．

言葉にするとあっけないですが，かなり面倒です．現在はデータ保存部だけとりあえず書き上げました．（まだまだバグが多いですが...）

今後の予定

あと少しバグ潰しをしたら，早速データ収集を始めたいと思います．とりあえずは2007年から始まったSuper Seriesのデータに絞って，色々いじってみたいと思います．こんなことしたいなー，というのはぼんやり考えてますが，まだそこまで固まってません．

このブログに読者がいるかはかなり怪しいところですが，もし解析して欲しいネタがあったらコメントで提供して頂けると嬉しいです．